人教版义务教育数学(七~九年级)新教材介绍
人教版《义务教育教科书数学》(七~九年级)以习近平新时代中国特色社会主义思想为指导,全面贯彻党的二十大精神和教育方针,落实立德树人根本任务;以《义务教育数学课程标准(2022年版)》为依据,落实“四基”,提升“四能”,发展核心素养,是一套在继承和借鉴基础上具有显著创新特点的教科书。
一、主编介绍
顾问:林群

中国科学院院士,中国科学院数学与系统科学研究院研究员。曾任中国数学会副理事长,国家自然科学基金委领导小组成员,全国人大代表。在泛函分析、计算数学等领域作出了一系列重要贡献。
顾问:田刚

中国科学院院士,北京大学讲席教授,国际数学联盟执委,民盟中央副主席,北京国际数学研究中心主任。曾任中国数学会理事长,北京大学校务委员会副主任,北京大学学术委员会副主任。在复几何、几何分析及数学物理等领域作出了一系列重要贡献。
主编:王长平

福建师范大学校长,第十四届全国政协委员,2017版高中数学课程标准和2022版义教数学课程标准修订组核心成员,中国数学会数学竞赛委员会副主任。
执行主编:李海东

人民教育出版社副总编辑,编审。中国教育学会中学数学教学专业委员会副理事长,《中小学数学》《中国数学教育》初中版主编。
二、教材介绍
(一)主要变化
1.完善结构与内容
根据课标变化,以及现行教材使用情况反馈,按照逻辑性、连续性、整体性、关联性的原则,构建了既符合数学逻辑,又符合学生心理逻辑的教科书体系,并调整了教材内容。例如,为了体现函数概念的重要性,将原教材中的“一次函数”章拆分为“函数”和“一次函数”两章;为了适应大数据时代,按照课标要求,在“数据的分析”章中增加“数据的四分位数”和“数据的分组”两节内容。
2.修订章节引言与章小结
为了更好地发挥教材的导学功能,全面修订了章节引言、小结等内容。包括遴选章节引言中的案例,完善主要内容、数学思想方法和学习(研究)方法的表述,更好地体现数学的本质;完善章小结的知识结构图,加强章小结的思想性与引导性,更好地帮助学生回顾反思。例如,在“圆”的章小结中,按照圆的有关概念、性质、计算,绘制了全面系统的本章知识结构图;基于圆与其他研究对象之间的关系、圆的特殊性质等角度,帮助学生回顾反思本章内容。
3.改进内容呈现方式
基于数学学科本质,改进内容呈现的方式方法,加强教材的思想性与联系性。以数学核心概念及其反映的思想方法为纽带,加强内容的纵横联系,通过类比、归纳、推广、特殊化等方式,使不同内容相互沟通,从而加深对数学的整体性认识。

“第二十一章 四边形”通过“特殊化”展开相关内容
4.加强综合与实践内容
综合与实践以小型活动与大型活动相结合的方式有层次地编排。在每章安排1~2个“数学活动”基础上,每册教材安排2个“综合与实践”,为学生开展跨学科学习提供教学资源。所选择综合与实践活动,主题涉及生活常识、科技、体育、工程、音乐、美术与建筑设计等多个方面,既考虑了活动内容所体现知识的综合性、与现实生活的联系性、跨学科的综合性,也考虑问题解决的开放性和拓展性。
5.注重数学文化
设置“溯源”“图说数学史”等栏目,以及在正文中有机融入数学文化,尤其注重中国数学文化的融入,使学生在学习数学知识的同时获得数学文化熏陶。例如,图说数学史“中国古代数学的光辉成就——解多元一次方程组”图文并茂地介绍了我国古代多元一次方程组的两种解法——直除法和互乘相消法,以及刘徽、贾宪、杨辉、梅文鼎等数学家在解多元一次方程组上的贡献,彰显了我国古代数学的光辉成就,体现了中华优秀传统数学文化。
6.优化问题情境
为了体现教材的联系性,从多个方面优化来自现实世界、数学世界、其他学科的问题情境。一是注重加强体现重大主题教育的素材,彰显国家意志;二是注重贴近学生日常生活,符合现实世界情况,激发学生的学习兴趣;三是符合学生的认知水平,确保学生认知活动的有效性;四是加强问题情境与问题解决之间的关联性,更好地体现问题情境的应用性。
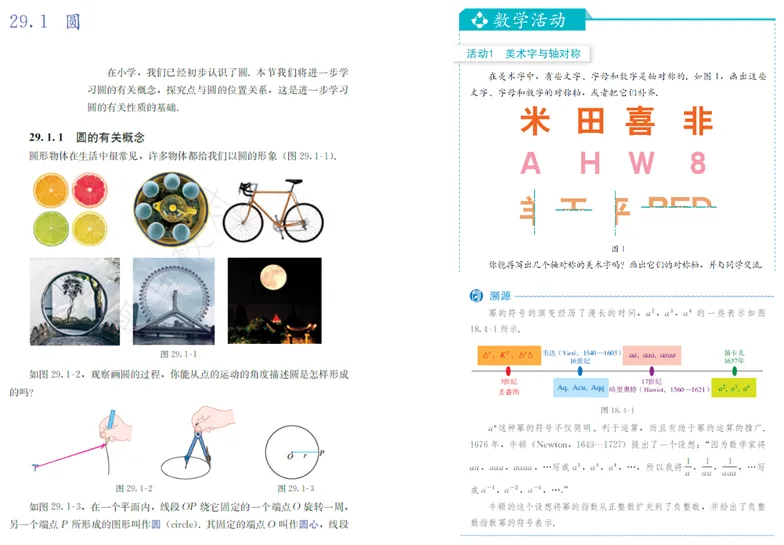
“圆”中的现实情境,“轴对称”中的其他学科情境,“分式”中的数学情境
7.升级例、习题系统
将例、习题系统(练习、习题、复习题)看成促进学生自主学习、提升创新意识、提高实践能力的重要平台。为更好地服务一线教学,整体考虑练习、习题、复习题的设置,从系统性、精确性、针对性、有效性、创新性、应用性等不同角度逐题进行审视与完善,并进行有层次地编排,全面升级例、习题系统。
8.提升插图质量
精选教材插图,确保插图清晰、准确,并能较好地体现必要性、真实性、美观性等特征。插图符合大众审美、反映数学学科特色,体现中国风、时代感、精气神、数学味;注重图文配合,反映内容本质,使呈现方式更加符合内容的教学过程与方法。例如,在“建筑中的数学”活动中,精美的插图对于数学美的体现令人印象深刻:“月光环”“水立方”体现出数学的简洁美,故宫、天坛体现出数学的对称美。
(二)主要特色
1.坚持德育为先、把握政治方向,体现教材的价值观
通过讲好两个故事,即“讲好中国贡献的数学故事,讲好数学呈现的中国故事”,在教材中有机融入习近平新时代中国特色社会主义思想,落实党的二十大精神,培育和践行社会主义核心价值观。贯彻落实重大主题教育,继承和弘扬中华优秀传统文化、革命文化和社会主义先进文化,加强生命安全与健康、国家安全和国防教育,渗透绿色发展等理念,体现教材的“培根铸魂”功能。例如,“平面直角坐标系”的章头图,展现了庆祝中华人民共和国成立70周年联欢活动中,天安门广场出现的“祖国万岁”壮观图案,其表演者点位还与平面直角坐标系中的有序数对相联系,能够将数学与学科德育有机融合。
2.聚焦核心素养、发展理性思维,体现教材的思想性
在体系结构上,既关注知识内容的数学逻辑,也关注学生学习的心理逻辑;既重视同一领域内容的逻辑关系,也关注不同领域内容之间的衔接和沟通;既考虑整体的螺旋上升,也考虑局部的直线深入,使教材具有良好的整体结构,让学生在不断的思考中,提高对重要数学思想和方法的理解水平。在内容的呈现上,关注数学知识所蕴含的思想、通性通法,以数学核心概念及其反映的基本思想为纽带,逻辑一致地呈现相关内容。
3.面向全体学生、关注发展差异,体现教材的发展性
教材既面向全体学生,也关注学生发展的差异。在保证基本要求的前提下,教材通过纳入课标带星号标记的选学内容,设置不同的选学栏目,正文设置探索性、开放性的问题等多种手段,体现出较好的弹性,能够满足学生的不同需求,落实“人人都能获得良好的数学教育,不同的人在数学上得到不同的发展”的课程理念,并便于教师发挥自己的教学创造性。
4.加强问题引导、展现思维过程,体现教材的过程性
教材以问题驱动学习,重视研究方法的引导,重视从“一般观念”出发构建对数学对象研究的思路,让学生经历“观察想象——实验探索——概括猜想——推理论证”的过程,从而发现规律、获得猜想、证明结论,学会用数学的思维思考现实世界。重视应用数学概念、性质解决问题的过程,运用数学原理对现实问题进行数学抽象,用数学语言表达数学问题,用数学方法构建模型解决问题,使学生学会用数学的语言表达世界。

“三角形全等的判定”以4个探究“问题串”展开数学对象的研究过程
5.重视背景应用、加强综合实践,体现教材的联系性
对于知识引入的背景和应用问题的素材,注重与数学知识的数学关联性、与学生现实生活的生活关联性、与其他学科的学科关联性。着重加强了跨学科综合与实践活动,从综合性、实践性、开放性等层面体现出与学生、学科的联系。注重以真实情境问题与过程性问题引领活动设置;注重以清晰的过程结构与任务说明指导活动实施;注重以结果性评价、过程性评价保证活动质量。
例如,“高铁列车运行中的数量关系”以方便人们出行活动的高铁列车为研究素材,通过向学生设置开放性的研究问题,对京沪线高铁列车的运行情况进行了多方面探讨。通过这个综合实践活动,有助于学生获得数学与物理学习的融合发展。
6.改进呈现方式、提升学习体验,体现教材的适切性
改进教材的栏目设置,通过章、节引言,具有思考性、探究性、综合性、开放性的栏目,以及教材边空,整体设计教材的问题系统,提出反映本质、自然连贯、难易适当、恰时恰点的问题串,为学生提供思考的空间、引导学生经历学习过程。重视不同数学语言的使用,充分利用语言文字、图表、数学图形、数学符号等多种形式,多元表征相关内容。版式设计充分利用四色印刷的优势,加强不同栏目、插图、文字用色的整体设计,使之更加生动、新颖、活泼、美观,提高教材的可读性和审美性,提升学生的阅读体验。
“勾股定理”一章中数、形、文字语言配合呈现,形成多元表征
7.精选主题素材、创新融入方式,体现教材的文化性
精选“历史与发展”“思想与方法”“人物与精神”“趣味与应用”等角度的数学文化主题,并重点关注我国传统数学在数学发展中的贡献,充分发挥数学的文化力量,引导学生认识数学的科学价值、应用价值和文化价值。
具体地,教材在正文中设置“溯源”栏目,结合正文内容的展开,让学生跨越时空,在追本溯源中自然地理解重要的概念和方法;通过教材边空,选配数学家画像,结合相关数学成就和人物故事,让学生感悟数学家的精神;设置“图说数学史”栏目,图文并茂地呈现数学发展的历史脉络,讲述重要概念的形成与发展,展示核心数学思想方法的演变进程等。
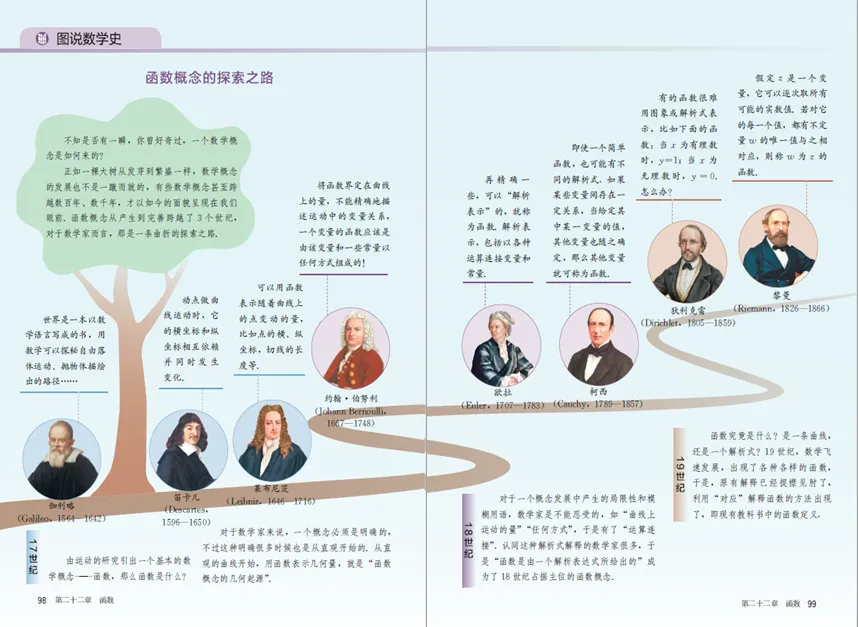
8.整合信息技术、改进教学方式,体现教材的融合性
教材注重信息技术与数学内容的深度融合,辅助数学探究,有效促进教学方式的改革。正文部分加强了信息技术工具的应用,利用它们完成复杂计算和绘图、展示动态变化过程、探索数学结论等,在实现信息技术与数学教材的深度融合上下功夫。设置“信息技术应用”栏目,让学生结合某一专题内容,利用信息技术工具发现规律、探究性质。此外,还利用边空给出使用信息技术的提示。例如,在“探究三角形全等条件”中,利用作图软件能够轻松获得不同三角形的角的度数,这为学生快速判断三角形全等提供了直观的数值依据。
